Octubre

Integración Compleja

En forma general las integrales complejas definen y tienen propiedades similares a la integración de números reales, sin embargo existen algunas integrales complejas que nos permitirán evaluar integrales reales.

CURVAS EN PLANO COMPLEJO

De acuerdo al tipo de gráfico y a la parametrización que se le otorgue al mismo, obtendremos una función z(t). La función z(t) depende de las definiciones de curvas en el plano complejo, para que pueda ser clasificada en:

• Curvas suaves
• Curvas simples o de Jordan
• Curvas no suaves 
• Curvas suaves por intervalos
• Curvas diferenciables
• Curvas rectificables

INTEGRALES DE LÍNEA

Estas integrales se definen para curvas suaves o suaves por intervalos. 

Propiedades.-

1. Sí ɣ es una curva suave o suave por intervalos y F(z) es continua, entonces Ǝ la integral de f(z) dz.

LONGITUD DE UNA CURVA

Sí ɣ es representada por z(t) = x(t) + i y(t) en a ≤ t ≤ b, su longitud se calcula:

INTEGRALES CERRADAS

Se calcula de igual forma que las integrales de línea, la principal diferencia es que en este caso las curvas ɣ son curvas cerradas.

Para el caso de variable compleja, estas funciones se resuelven por el teorema de Cauchy y las integrales de Cauchy.

Propiedades.-

1. Teorema de la Integral de Cauchy.

Sea f(z) una función analítica en D, un dominio simplemente conexo y C una curva cerrada simple en D, entonces:

    2.  Teorema de la Deformación.

Sea f(z) una función analítica en D, excepto en Zo y sean C1 y C2 curvas cerradas simples que encierran a Zo, entonces:

INTEGRALES DE CAUCHY

Si f es analítica en un dominio simplemente conexo D. Sea C curva cerrada simple en D que encierra a Zo, entonces: 

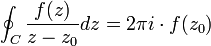
SUCESIONES Y SERIES DE VARIABLE COMPLEJA

Las sucesiones y series de variable compleja son similares a las de variable real. Sólo la serie de Laurent es propia y únicamente definida para variable compleja.

SUCESIONES.-  Las sucesiones complejas son funciones de números naturales (N) en los números complejos (C).

• Se denota por {Zn}
• Es un listado de cada uno de los elementos de que cumple con la condición especificada

{Zn} = i ^ n

SERIES.- Si sumamos los términos de una sucesión obtendremos una serie.

La convergencia de una serie compleja se determina mediante el análisis de la convergencia de las series reales que lo conforman.